Abstract

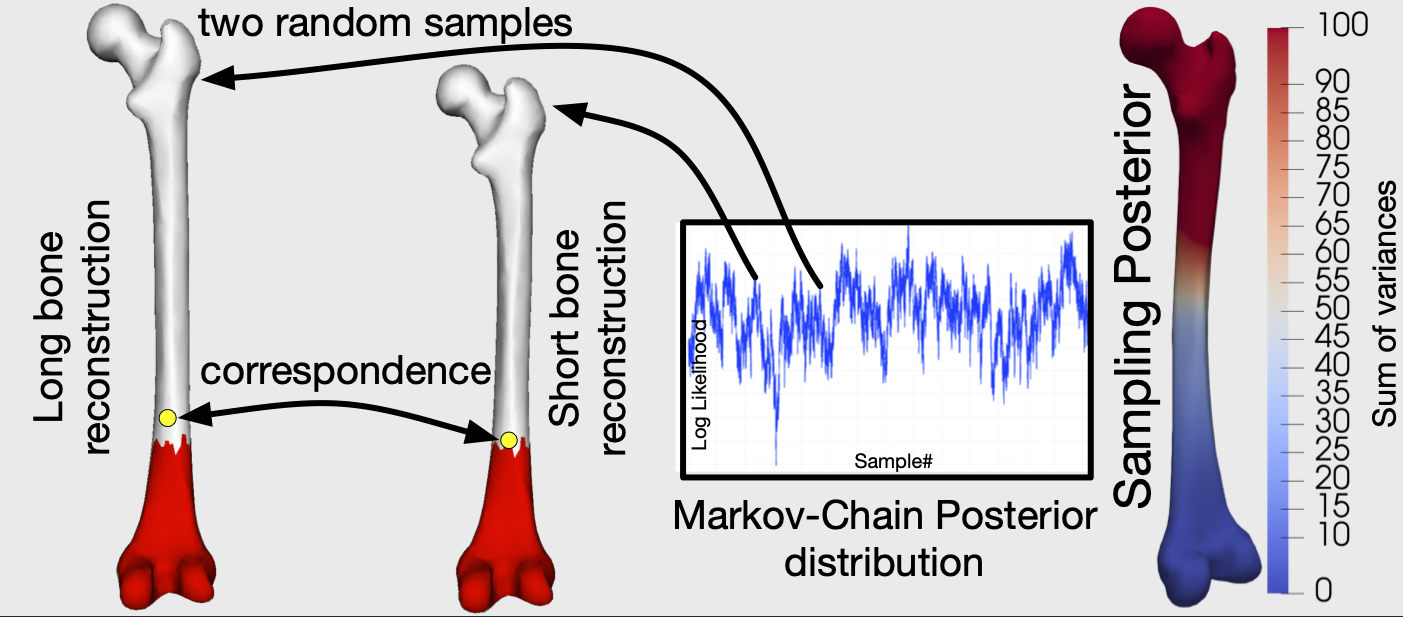
We frequently encounter the need to reconstruct the full 3D surface from a given part of a bone in areas such as orthopaedics and surgical planning. Once we establish correspondence between the partial surface and a Statistical Shape Model (SSM), the problem has an appealing solution. The most likely reconstruction, as well as the full posterior distribution of all possible surface completions, can be obtained in closed form with an SSM. In this paper, we argue that assuming known correspondence is unjustified for long bones. We show that this can lead to reconstructions, which greatly underestimate the uncertainty. Even worse, the ground truth solution is often deemed very unlikely under the posterior. Our main contribution is a method which allows us to estimate the posterior distribution of surfaces given partial surface information without making any assumptions about the correspondence. To this end, we use the Metropolis-Hastings algorithm to sample reconstructions with unknown pose and correspondence from the posterior distribution. We introduce a projection-proposal to propose shape and pose updates to the Markov-Chain, which lets us explore the posterior distribution much more efficiently than a standard random-walk proposal. We use less than 1% of the samples needed by a random-walk to explore the posterior. We compare our method with the analytically computed posterior distribution, which assumes fixed correspondence. The comparison shows that our method leads to much more realistic posterior estimates when only small fragments of the bones are available.